¿Qué es?
Es una ampliación de la Lenguaje de enunciados que cuenta con un lenguaje formal más rico (más expresivo) y con un conjunto de reglas que permiten validar razonamientos expresados utilizando este lenguaje. La Lenguaje de enunciados se debe entender, a partir de este momento, como un subconjunto de la lógica de predicados.
¿Cuál es su alfabeto?
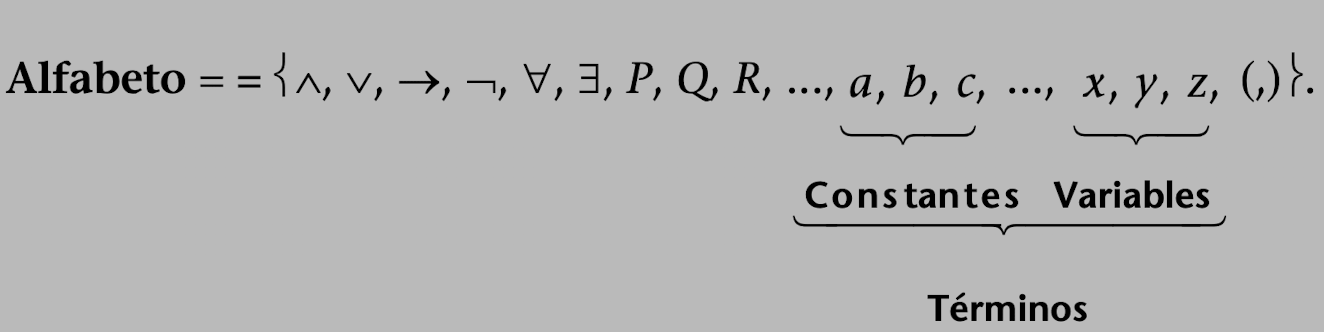
¿Cómo se construyen las fórmulas?
Las reglas siguientes definen cómo hay que construir fórmulas correctamente a partir de los elementos básicos:
- Si P es un símbolo de predicado y t1,…, tn (n >= 0) son símbolos de términos, entonces P(t1,…,tn) es una fórmula. Estas fórmulas también se denominan átomos o fórmulas atómicas.
- Si B y A son fórmulas, entonces (⌝A), (A ∧ B), (A ∨ B) y (A → B) también son fórmulas.
- Si A es una fórmula y x es una variable, entonces (∀x A) y (∃x A) también son fórmulas.
- A excepción de los casos expuestos anteriormente, no hay ninguna otra fórmula.